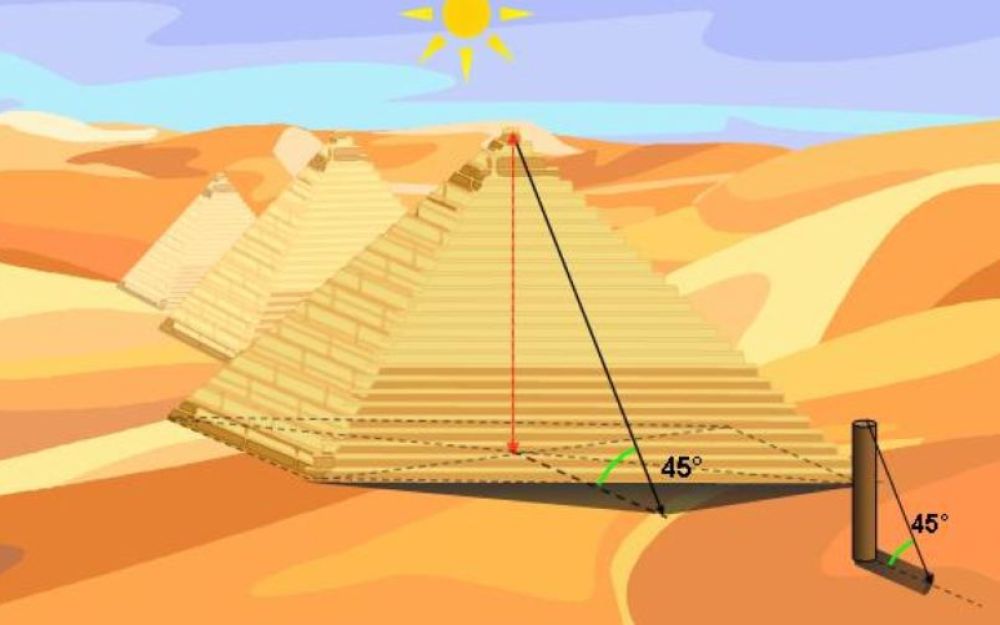
Gli antichi la sapevano lunga! Così diceva mio nonno Battista. Già nel VI secolo a.C. Talete riuscì a calcolare l’altezza della piramide di Cheope con un bastone. Poniamo di avere un’asta della lunghezza di un metro. Accade che d’estate, durante la giornata, la lunghezza del bastone e quello della sua ombra siano uguali. Guarda caso ciò accade quando il Sole è a un’altezza di 45°. È allora sufficiente misurare l’ombra proiettata dalla piramide e applicare una proporzione facilmente intuibile. Quante ombre del bastone servono per coprire la lunghezza dell’ombra della piramide? Poiché, a oggi, l’ombra della piramide è circa 138 volte quella del bastone la sua altezza sarà 138 metri!

Naturalmente, per comodità della misura, con una corda e un punteruolo possiamo semplicemente tracciare una circonferenza attorno al bastone con raggio uguale alla lunghezza del bastone stesso. Quando l’ombra del bastone tocca la circonferenza è il momento di segnare dove finisce l’ombra della piramide. La nostra misura risulterà essere tanto più precisa quanto il piano dell’ombra sarà il più orizzontale possibile e, nondimeno, quanto il bastone sarà stato tenuto esattamente in posizione verticale.

Proviamo ora a fare qualcosa di più complicato. Misuriamo la distanza di una finestra dalla parete posta di fronte a noi: poniamo 540 cm. Poi, sempre con le spalle alla parete, prendiamo un righello e lo posizioniamo distante dagli occhi fin tanto che il lato della finestra che abbiamo di fronte e che vogliamo determinare misuri 10 cm; durante questa rilevazione dobbiamo anche misurare la distanza tra i nostri occhi e il righello: 33 cm. Calcoliamo ora il rapporto tra queste due misurazioni: 540 cm diviso 33 cm uguale 16,36. Se moltiplichiamo questo valore per 10 cm otteniamo la lunghezza del lato della finestra che ci interessa: 163,6 cm! Lo andiamo subito a misurare: ha proprio questo valore. In effetti se facciamo combaciare – partendo dai nostri occhi – lo 0 del righello e l’inizio del lato della finestra e, similmente, il valore di 10 del righello e la fine del lato della finestra, formiamo due triangoli simili che hanno tutti gli angoli uguali e i lati in proporzione. Il primo è quello tra i nostri occhi e i 10 cm del righello che ne rappresenta la base, mentre il secondo triangolo è quello tra i nostri occhi e il lato della finestra che rappresenta la base del secondo triangolo: il rapporto tra le due basi dei triangoli è uguale al rapporto tra le loro altezze.

Similmente con un righello, un metro e un gettone riusciamo a stimare il diametro della Luna. Prendiamo un gettone che si usa per i carrelli del supermercato: il suo diametro è di circa 2,6 cm. In una notte di Luna piena lo allontaniamo dai nostri occhi fino a coprire, non senza difficoltà e aiutandoci con un lungo palo di legno quadrato e dei cavalletti (nonché qualche amico), la circonferenza lunare. Ciò accade quando il gettone è distante, dai nostri occhi, circa 300 cm. Sapendo che la Terra dista dalla Luna 384.400 km e applicando il procedimento già utilizzato, dopo aver trasformato tutto in km otteniamo il seguente risultato: (384.400/0,00300) × 0,000026 = 3.331 km. Un valore che sottostima di 144 km in valore reale (con un errore inferiore al 4,2%): non male, viste le difficoltà!

Naturalmente con un procedimento del tutto simile, conoscendo il valore del diametro della Luna, possiamo ricavarne la distanza dalla Terra.

di Erminio Milanesi